Grafos y sus representaciones

Un grafo \(G\) consiste de un conjunto finito \(V\), cuyos miembros son llamados vértices, y un conjunto de 2-subconjuntos de \(V\), cuyos miembros son aristas

Escribimos \(G = (V, E)\) para denotar un grafo \(G\) con conjunto de vértices \(V\) y conjunto de aristas \(E\).

Un ejemplo de un grafo \(G = (V, E)\) dado por los conjuntos:

La representación pictórica de un grafo puede ser más fácil de entender a simple vista:

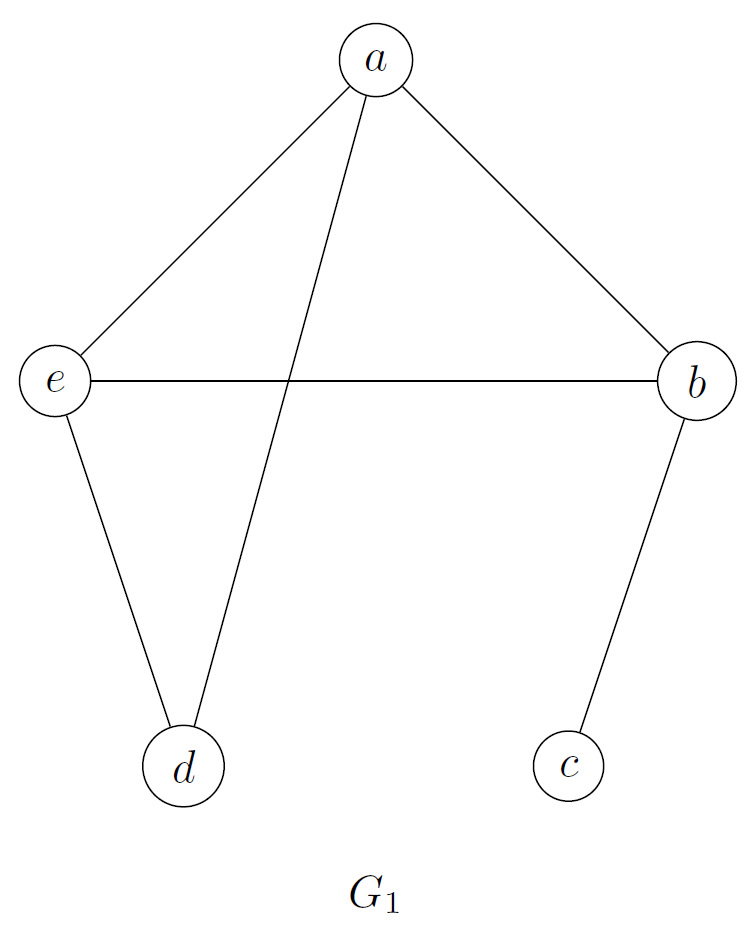
Sin embargo esta representación no es útil para comunicarse con una computadora. Debe representarse mediante conjuntos o una tabla.

Los vértices \(x, y\) de un grafo son adyacentes cuando \(\{x, y\}\) es una arista.

Podemos representar un grafo \(G = (V, E)\) por su lista de adyacencia, donde cada vértice \(v\) encabeza una lista de los vértices adyacentes a \(v\):

Este grafo podría representarse en Python como:

grafo = {
  "a": ["b", "d", "e"],
  "b": ["c", "a", "e"],
  "c": ["b"],
  "d": ["a", "e"],
  "e": ["b", "d", "a"]
}

Isomorfismo de grafos

Dos grafos \(G_1\) y \(G_2\) son isomorfos si existe una biyección \(\alpha\) entre el conjunto de vértices de \(G_1\) y \(G_2\) tal que
Si \(\{x, y\}\) es una arista en \(G_1\) entonces \(\{\alpha(x), \alpha(y)\}\) es una arista en \(G_2\).
Si \(\{z, w\}\) es una arista en \(G_2\) entonces \(\{\alpha^{-1}(z), \alpha^{-1}(w)\}\) es una arista en \(G_1\).

Por ejemplo:

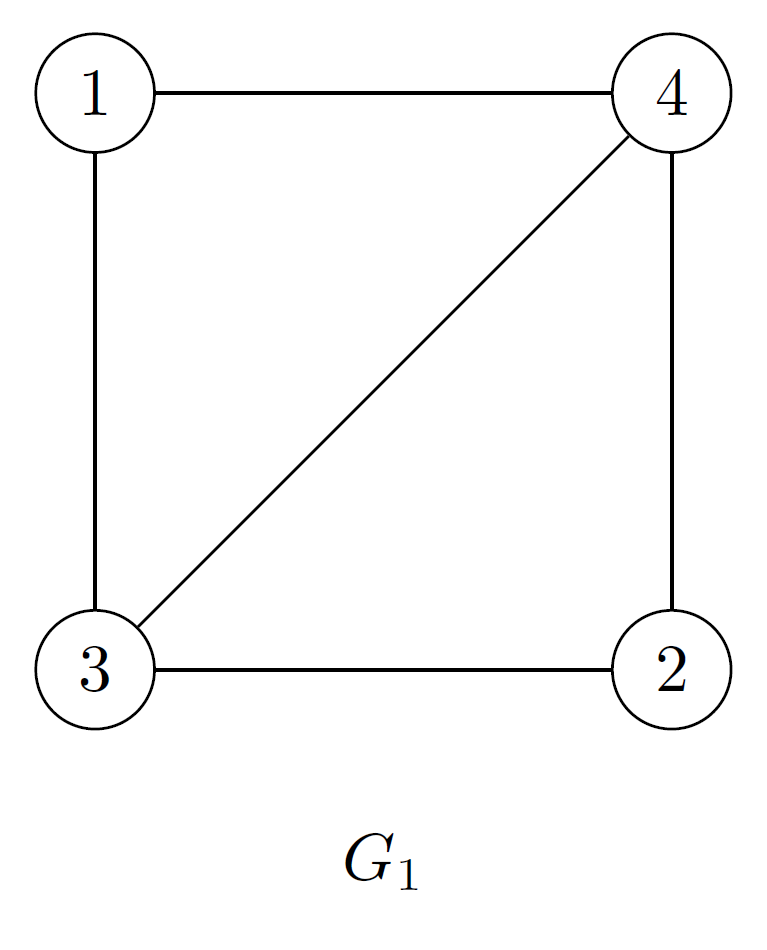
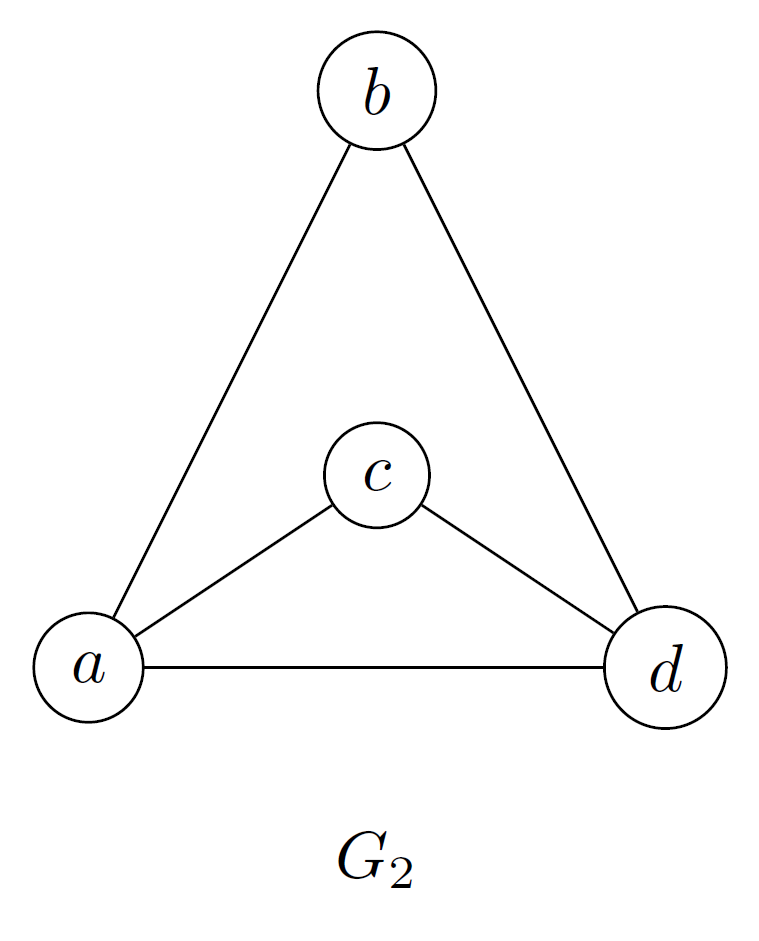
La biyección es dada por:

Comprobando que a cada arista en \(G_1\) le corresponde una arista de \(G_2\) y viceversa.

Si dos grafos tienen diferente cantidad de vértices, entonces no pueden ser isomorfos. Si tienen la misma cantidad de vértices, pero diferente cantidad de aristas, entonces hay biyecciones de vértices pero ninguna de estas puede ser un isomorfismo.

Determinar la igualdad de dos grafos puede ser una tarea computacional costosa dependiendo de la cantidad de vértices y aristas.

Subgrafos

Sea \(G = (V, E)\) un grafo. Un subgrafo de \(G\) es un grafo \(G' = (V', E')\) donde \(V' \subset V\) y \(E' \subset E\).

Podemos determinar si dos grafos no son isomorfos en base a sus subgrafos:

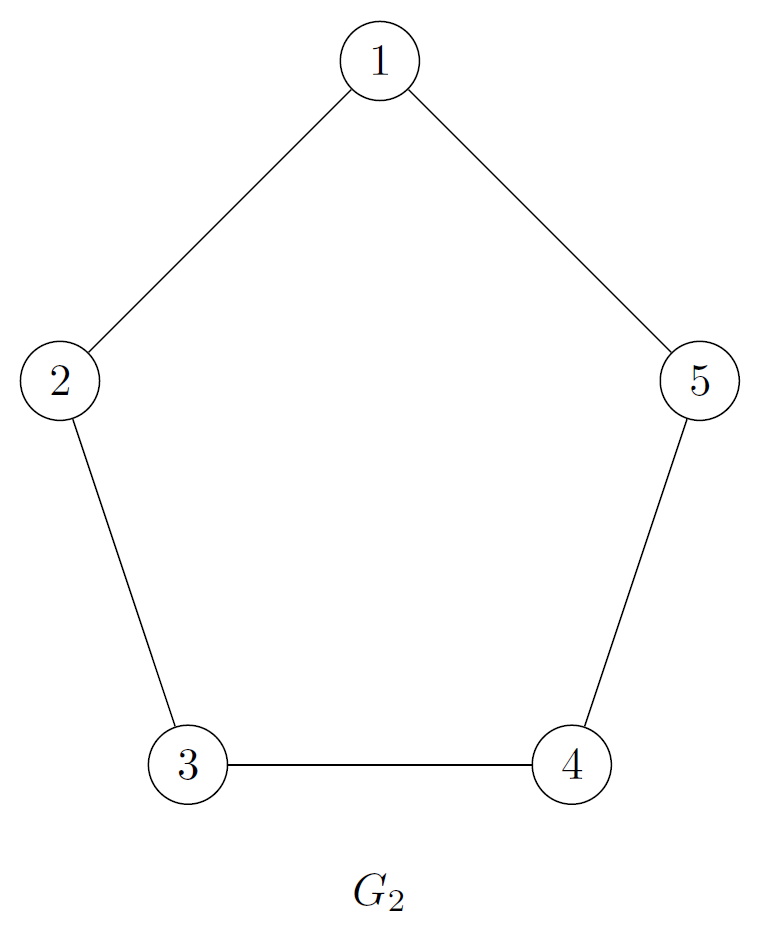
Hay un subgrafo \(K_1 \subset G_1\) que contiene 1 arista. Pero \(K_1 \not\subset G_2\). Por lo tanto, \(G_1\) y \(G_2\) no son isomorfos.

Valencias

La valencia de un vértice \(v\) en un grafo \(G = (V, E)\) es el número de aristas que tienen a \(v\) como extremo. Se utiliza la notación \(\delta(v)\) para la valencia de \(v\).

En una lista de adyacencia, la valencia de un vértice es la cantidad de elementos de la columna del vértice:

Diremos que un vértice es par si su valencia es par, e impar si su valencia es impar.

Handshaking lemma

La suma de las valencias de los vértices de un grafo \(G = (V, E)\) es igual al doble de la cantidad de aristas de \(G\).

Por ejemplo, en base a la lista de valencias anterior:

No existe un grafo que pueda contradecir esta propiedad.

Grafos regulares, planares y conexos

Un grafo regular es aquel con la misma valencia \(r\) en todos sus vértices.

Un grafo planar es aquel donde no se cruzan las aristas.

Un grafo conexo es aquel donde no hay vértices aislados.

Un ejemplo que cumple ambas condiciones es este grafo:

Árboles

Un grafo \(G = (V, E)\) es árbol si es conexo y sin ciclos, tal que \(|E| = |V| - 1\) y donde cada par de vértices está conectado por un único camino.

Un árbol sin vértices es un árbol vacío. Un árbol con vértices tiene un vértice especial llamado raíz, del cual pueden derivarse otros vértices estableciendo una jerarquía o relación de dependencia entre ellos.

En Haskell, podríamos definir un árbol binario de búsqueda, donde partiendo de un nodo o vértice podemos obtener como máximo, dos adyacentes:

data ABB a = Vacio | Nodo a (ABB a) (ABB a) deriving (Show)

Una representación podría ser:

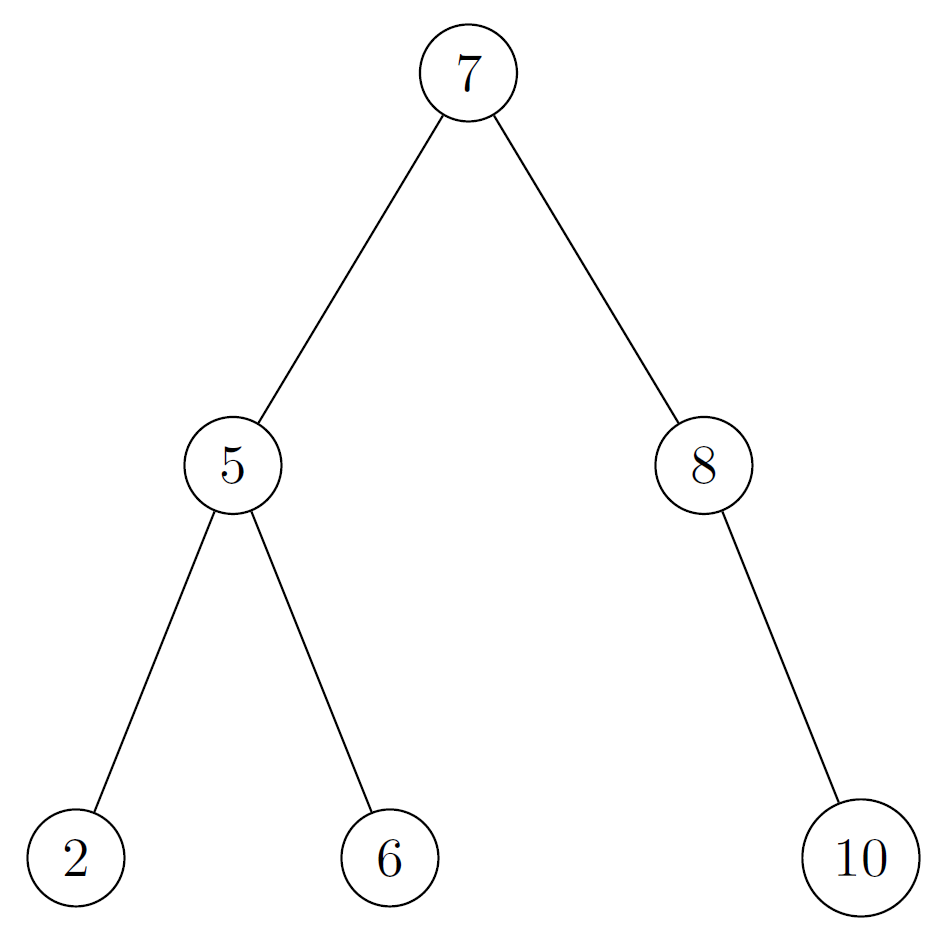
En este tipo de árbol se cumple que los valores del subárbol izquierdo son menores al valor del nodo raíz, y los valores del subárbol derecho son mayores al valor del nodo raíz.

Ciclos, caminos y caminatas

Una caminata en un grafo \(G\) es una secuencia de vértices \(v_0, v_1, \ldots, v_k\) tal que \(\{v_i, v_{i+1}\}\) es una arista de \(G\) para \(0 \leq i < k\).

Un camino es una caminata donde todos los vértices son distintos.

Un ciclo es una caminata \(v_0, v_1, \ldots, v_k, v_0\) (Se repite el primer vértice al final).

Algunos ejemplos en el grafo \(G_1\) anterior son:

• \(a, d, e, b, c\) es un camino.

• \(c, b, a, d, b\) es una caminata.

• \(a, b, e, d, a\) es un ciclo.

Ciclo Hamiltoniano

Un ciclo Hamiltoniano en un grafo \(G\) es un ciclo que pasa por todos los vértices de \(G\) exactamente una vez.

Caminata Euleriana

Una caminata Euleriana en un grafo \(G\) es una caminata que usa todas las aristas de \(G\) exactamente una vez.

Coloreo de grafos

Un coloreo de un grafo \(G = (V, E)\) es una función \(c: V \rightarrow S\) donde \(S\) es un conjunto de colores. El número cromático de \(G\) es el mínimo número de colores necesarios para colorear \(G\).

La función de coloreo cumple la propiedad:

Es decir, dos vértices adyacentes no pueden tener el mismo color. Si bien no existe un algoritmo definitivo para determinar el número cromático de un grafo, podemos usar el Algoritmo Greedy para obtener una aproximación.

Algoritmo Greedy

Si hay vértices no coloreados, elegimos un vértice sin color y le otorgamos un color que no tengan sus vecinos.

Primero definimos un orden a los vértices: \(v_0, v_1, \ldots, v_n\). Definimos \(S\) como el conjunto de colores.

• Le damos el color \(0\) a \(v_0\).
• Tomamos el siguiente vértice, y le damos el color más bajo que no tengan sus vecinos.
• Al terminar el último vértice, el número cromático es el cardinal de \(S\).

Ejercicios resueltos - Grafos

1.

Dar los componentes/subgrafos del grafo cuya lista de adyacencias es:

Podemos dibujar los siguientes subgrafos \(G_1, G_2\):

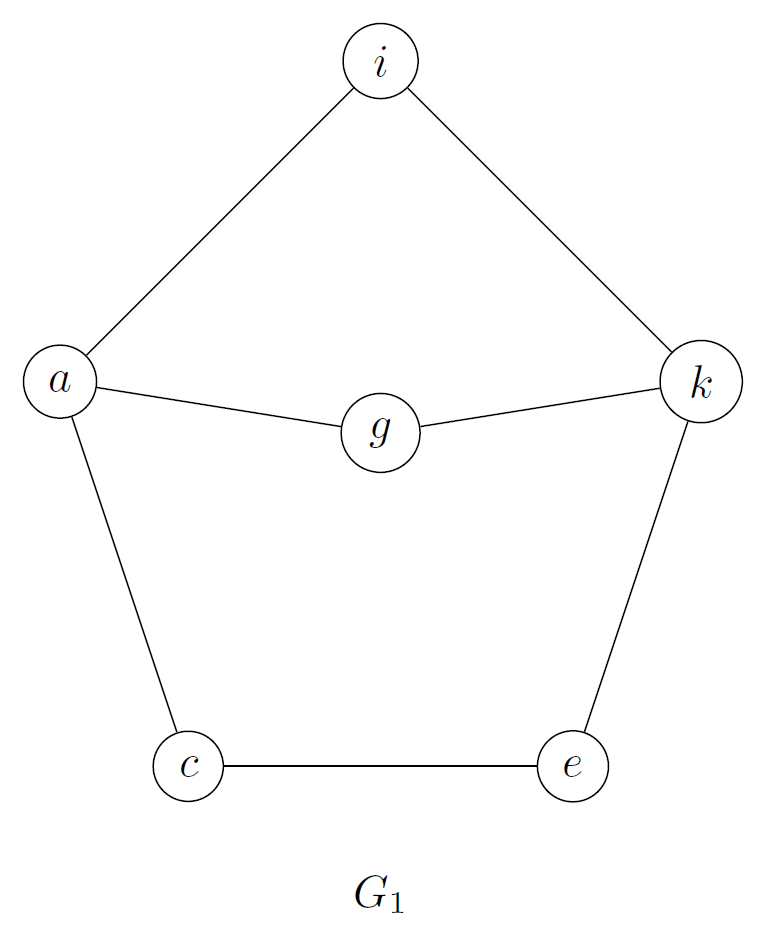
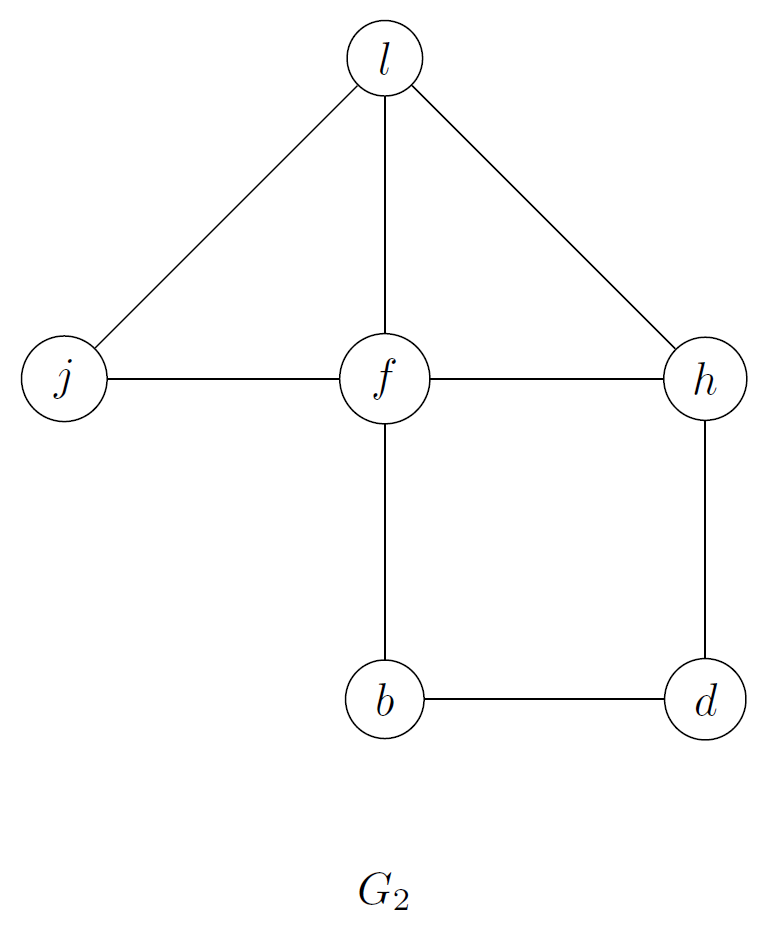
2.

Determinar si los subgrafos \(G_1, G_2\) son isomorfos.

Podemos determinar que no son isomorfos, observando el vértice \(f\) hay un subgrafo \(K_4 \subset G_2\) que contiene 4 aristas y \(K_4 \not\subset G_1\).

3.

Determinar si alguno de los subgrafos tiene un ciclo Hamiltoniano.

El subgrafo \(G_2\) tiene un ciclo Hamiltoniano que pasa por todos los vértices exactamente una vez:

4.

Aplicar el Algoritmo Greedy para colorear \(G_1, G_2\) y dar sus números cromáticos.

Para aplicar el Algoritmo Greedy en \(G_1\), podemos seguir el siguiente orden:

Ahora aplicamos los pasos del Algoritmo:

• 1) \(\; i\) tiene colores vecinos \(S = \emptyset \implies c(i) = 0\).
• 2) \(\; e\) tiene colores vecinos \(S = \emptyset \implies c(e) = 0\).
• 3) \(\; k\) tiene colores vecinos \(S = \{0\} \implies c(k) = 1\).
• 4) \(\; c\) tiene colores vecinos \(S = \{0\} \implies c(c) = 1\).
• 5) \(\; a\) tiene colores vecinos \(S = \{0, 1\} \implies c(a) = 2\).
• 6) \(\; g\) tiene colores vecinos \(S = \{1, 2\} \implies c(g) = 3\).

Por lo tanto, el número cromático de \(G_1\) es \(3\). Podría colorearse de la siguiente forma:

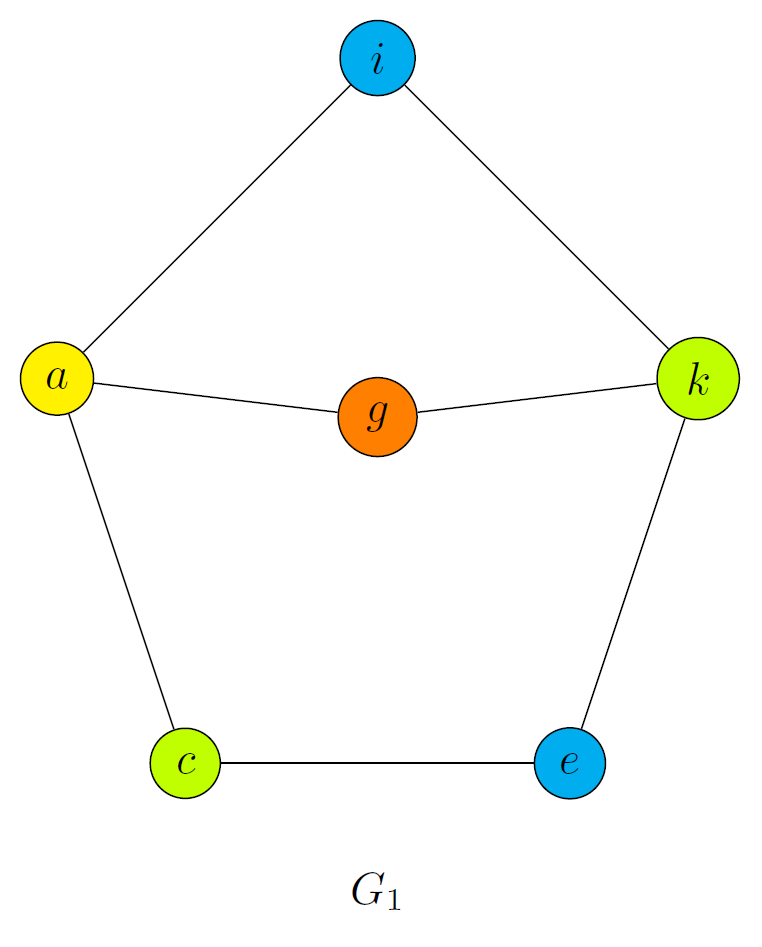
Para \(G_2\), podemos seguir el siguiente orden:

Aplicando los pasos del Algoritmo:

• 1) \(\; l\) tiene colores vecinos \(S = \emptyset \implies c(l) = 0\).
• 2) \(\; d\) tiene colores vecinos \(S = \emptyset \implies c(d) = 0\).
• 3) \(\; h\) tiene colores vecinos \(S = \{0\} \implies c(h) = 1\).
• 4) \(\; b\) tiene colores vecinos \(S = \{0\} \implies c(b) = 1\).
• 5) \(\; j\) tiene colores vecinos \(S = \{0\} \implies c(j) = 1\).
• 6) \(\; f\) tiene colores vecinos \(S = \{0, 1\} \implies c(f) = 2\).

Por lo tanto, el número cromático de \(G_2\) es \(2\). Podría colorearse de la siguiente forma:

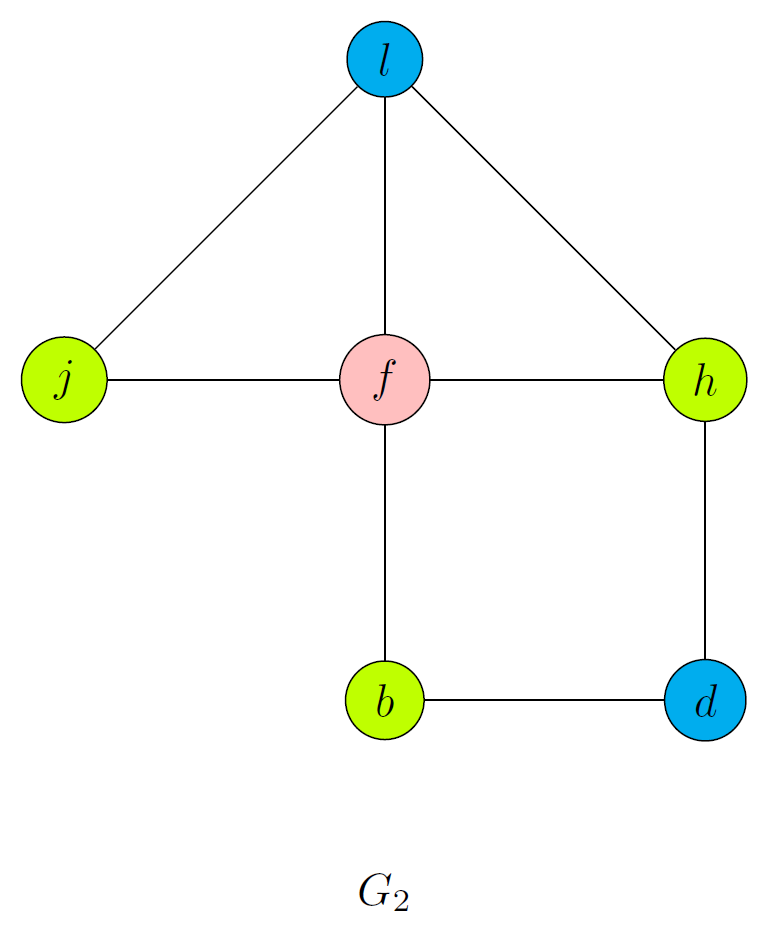
5.

Determinar las valencias de todos los vértices en \(G_1, G_2\):