Funciones (AM1)
Una función \(f\) es una regla que asigna a cada elemento \(x \in A\) un unico elemento \(y \in B\).
Dominio, Codominio e Imagen
\[f: A \rightarrow B \]- \(A\) es el dominio de \(f\) (Conjunto de salida).
- \(B\) es el codominio de \(f\) (Conjunto de llegada).
- Aplicamos la función en los elementos del dominio para encontrar los elementos del codominio, \(f(x)=y\).
El Dominio incluye los valores de \(x\) en los que \(f\) está definida y PUEDE usar.
El Codominio incluye valores de \(y\) que \(f\) PODRÍA tomar.
La Imagen es el conjunto de valores de \(y\) que \(f\) REALMENTE toma.
Encontrar el Dominio
Para encontrar el dominio de una función, debemos pensar en los valores que la misma está definida.
- Ejemplo 1: \(f(x) = \frac{1}{3 - x}\)
La función está definida para todos los valores de \(x\) excepto para aquellos que hacen que el denominador sea cero.
Podemos igualar el denominador a 0 y resolver la ecuación: \(3 - x = 0 \Rightarrow x \neq 3\).
Por lo que el \(Dom\;f(x) = \mathbb{R} - \{3\}\).
- Ejemplo 2: \(f(x) = \sqrt{x-1}\)
La raiz cuadrada está definida para valores mayores o iguales a cero.
En este caso podemos usar la siguiente desigualdad y resolverla: \(x-1 \geq 0 \Rightarrow x \geq 1\)
Por lo que el \(Dom\;f(x) = [1, \infty)\).
Encontrar la Imagen
Para encontrar la imagen de una función, debemos pensar en los valores que la misma toma.
- Ejemplo 1: \(f(x) = x^2\)
La función toma todos los valores de \(y\) mayores o iguales a cero.
Por lo que la \(Im\;f(x) = [0, \infty)\).
- Ejemplo 2: \(f(x) = \frac{1}{x}\)
La función toma todos los valores de \(y\) excepto el cero.
Por lo que la \(Im\;f(x) = \mathbb{R} - \{0\}\).
Funciones Elementales
Esta calculadora de geogebra muestra las funciones elementales y más usadas en la materia (puede resultar útil para experimentar y modificar las funciones):
Funciones Pares e Impares
\(f\) es par si \(f(-x) = f(x)\), impar si \(f(-x) = -f(x)\).
Simétrica o asimétrica en el eje \(y\), respectivamente. Puede no ser par/impar.
Por la anterior definición, debemos evaluar la función en \(-x\) y comparar.
Ejercicios resueltos - Funciones pares e impares
1.
Determinar si \(f(x) = x^2\) es par, impar o ninguna de las dos.
\[f(-x) = (-x)^2 \]El cuadrado de un número es positivo:
\[f(-x) = x^2 = f(x) \]Por lo que \(f\) es par.
2.
Determinar si \(f(x) = x^3\) es par, impar o ninguna de las dos.
\[f(-x) = (-x)^3 \]Si el exponente es impar, el resultado es negativo:
\[f(-x) = -x^3 = -f(x) \]Por lo que \(f\) es impar.
3.
Determinar si \(f(x) = x + 1\) es par, impar o ninguna de las dos.
\[\begin{array}{ll} f(-x) = -x + 1, \\ f(-x) \neq f(x) \end{array} \]\(f\) no es par,
\[\begin{array}{ll} -f(x) = -(x + 1) = -x - 1, \\ -f(x) \neq f(-x) \end{array} \]\(f\) tampoco es impar. Por lo tanto, ninguna de las dos.
Composición de funciones
Dadas dos funciones \(f\) y \(g\), la composición de \(f\) con \(g\) es la función \(f \circ g\) definida por \((f \circ g)(x) = f(g(x))\).
Dadas las siguientes funciones:
\[f(x) = \frac{1}{x},\;\;g(x) = \sqrt{x} \]Evaluamos \(g(x)\) en \(f(x)\):
\[(f \circ g)(x) = f(g(x)) = \frac{1}{g(x)} = \frac{1}{\sqrt{x}} \]Damos con el dominio de \(f\) y \(g\):
\[\begin{align} Dom\;f(x) &= \mathbb{R} - \{0\}, \\ Dom\;g(x) &= [0, \infty) \end{align} \]Por lo tanto, \(Dom\;(f \circ g)(x) = \mathbb{R} - \{0\} \cap [0, \infty) = (0, \infty)\)
Ejercicios resueltos - Composición de funciones
1.
Dadas las funciones \(f(x) = x^2\) y \(g(x) = \sqrt{x}\), calcular \((f \circ g)(x)\) y dar su dominio.
\[(f \circ g)(x) = f(g(x)) \]Reemplazamos \(x\) por \(g(x)\):
\[(f \circ g)(x) = (g(x))^2 \]Reemplazamos \(g(x)\) por \(\sqrt{x}\) y resolvemos:
\[(f \circ g)(x) = (\sqrt{x})^2 = x \]El \(Dom\;f(x) = \mathbb{R}\) y el \(Dom\;g(x) = [0, \infty)\)
Por lo tanto, \(Dom\;(f \circ g)(x) = \mathbb{R} \cap [0, \infty) = [0, \infty)\)
2.
Dadas las funciones \(f(x) = \frac{1}{5x-2}\) y \(g(x) = \sqrt{x}\), calcular \((g \circ f)(x)\) y dar su dominio.
\[(g \circ f)(x) = g(f(x)) \]Reemplazamos \(x\) por \(f(x)\):
\[(g \circ f)(x) = \sqrt{f(x)} \]Reemplazamos \(f(x)\) por \(\frac{1}{5x-2}\) y resolvemos:
\[(g \circ f)(x) = \sqrt{\frac{1}{5x-2}} \]Igualamos el denominador por 0 y resolvemos:
\[5x-2 = 0 \Rightarrow x \neq \frac{2}{5} \]El \(Dom\;f(x) = \mathbb{R} - \{\frac{2}{5}\}\) y el \(Dom\;g(x) = [0, \infty)\)
Por lo tanto, \(Dom\;(g \circ f)(x) = \mathbb{R} - \{\frac{2}{5}\} \cap [0, \infty) = [0, \frac{2}{5}) \cup (\frac{2}{5}, \infty)\)
3.
Dada la función \(f(x) = \frac{1}{x}\), calcular \((f \circ f)(x)\) y dar su dominio.
\[(f \circ f)(x) = f(f(x)) \]Reemplazamos \(x\) por \(f(x)\):
\[(f \circ f)(x) = f(f(x)) = f(\frac{1}{x}) = \frac{1}{\frac{1}{x}} = x \]El \(Dom\;f(x) = \mathbb{R} - \{0\}\)
Por lo tanto, \(Dom\;(f \circ f)(x) = \mathbb{R} - \{0\}\)
Funciones Inyectivas, Sobreyectivas y Biyectivas
Una función \(f\) es inyectiva si \(f(x_1) = f(x_2) \Rightarrow x_1 = x_2\) (si 2 elementos del dominio no tienen igual imagen).
Una función \(f\) es sobreyectiva si \(Im\;f(x) = Codom\;f(x)\).
Una función \(f\) es biyectiva si es inyectiva y sobreyectiva.
Tomemos la siguiente función: \(f : \mathbb{R} \rightarrow \mathbb{R}\), \(f(x) = x^2\).
\(f\) es inyectiva?
Evaluamos en \(x_1\) y \(x_2\), los igualamos:
\[f(x_1) = f(x_2) \]Luego, reemplazamos \(x\) por \(x^2\) (el subíndice permanece):
\[x_1^2 = x_2^2 \]Igualamos a 0 y resolvemos:
\[x_1^2 - x_2^2 = 0 \]Aplicamos diferencia de cuadrados:
\[(x_1 - x_2)(x_1 + x_2) = 0 \]Si \(ab = 0\) entonces \(a = 0\) o \(b = 0\):
\[(x_1 - x_2 = 0)\;\lor\;(x_1 + x_2 = 0) \]Resolvemos ambos casos:
\[x_1 = x_2\;\lor\;x_1 = -x_2 \]Por lo tanto, \(f\) no es inyectiva. No se cumple que \(x_1 = x_2\) en todos los casos.
Si trazamos una recta horizontal en el gráfico de una función inyectiva, esta solo cortará a la función en un punto. Lo cual no sucede en el ejemplo anterior.
\(f\) es sobreyectiva?
\(x^2\) solo toma valores positivos o cero. Por lo tanto, \(Im\;f(x) = [0, \infty)\).
Pero el \(Codom\;f(x) = \mathbb{R}\). Por lo tanto, \(Im\;f(x) \neq Codom\;f(x)\), \(f\) no es sobreyectiva.
Función Inversa
Dada una función \(f\), la función inversa \(f^{-1}\) es la función que cumple \(f^{-1}(f(x)) = x\).
Una función \(f\) tiene inversa \(\iff\) es biyectiva.
Dada la función \(g : \mathbb{R} \rightarrow \mathbb{R}\), \(g(x) = 3x\).
Esta función es biyectiva, cumple con las propiedades anteriores. Por lo tanto, tiene inversa.
Para encontrar la función inversa, despejamos \(x\):
\[\begin{array}{ll} y & = 3x \\ \frac{y}{3} & = x \end{array} \]Luego, intercambiamos el lugar de las variables:
\[\frac{x}{3} = y \]Por lo tanto, \(g^{-1}(x) = \frac{x}{3}\).
Ejercicios resueltos - Funciones inversas
1.
Dada la función \(g : \mathbb{R} \rightarrow \mathbb{R}\), \(g(x) = x + 3\), encontrar (si es posible) \(g^{-1}\).
\(g\) es biyectiva?
\(g\) es inyectiva, ya que \(x_1 + 3 = x_2 + 3 \Rightarrow x_1 = x_2\).
\(g\) es sobreyectiva, ya que \(Im\;g(x) = \mathbb{R}\).
Por lo tanto, \(g\) es biyectiva.
Ahora podemos encontrar la función inversa con la fórmula anterior:
\[y = x + 3 \]Despejamos \(x\) (restar 3 en ambos lados):
\[x = y - 3 \]Intercambiamos el lugar de las variables:
\[y = x - 3 \]La función inversa es \(g^{-1}(x) = x - 3\).
2.
Determinar solo si \(h(x) = \frac{3x - 4}{x + 1}\) es inyectiva y encontrar su inversa.
Para saber si \(h\) es inyectiva, evaluamos en \(x_1\) y \(x_2\), los igualamos:
\[h(x_1) = h(x_2) \]Luego, reemplazamos \(x\) por \(x_1\) y \(x_2\):
\[\frac{3x_1 - 4}{x_1 + 1} = \frac{3x_2 - 4}{x_2 + 1} \]Multiplicamos ambos miembros por \((x_1 + 1)(x_2 + 1)\):
\[(3x_1 - 4)(x_2 + 1) = (3x_2 - 4)(x_1 + 1) \]Resolvemos la ecuación:
\[3x_1x_2 + 3x_1 - 4x_2 - 4 = 3x_2x_1 + 3x_2 - 4x_1 - 4 \]Simplificamos:
\[3x_1 - 4x_2 = 3x_2 - 4x_1 \]Sumamos \(4x_2\) y \(4x_1\) en ambos miembros:
\[7x_1 = 7x_2 \]Dividimos por \(7\) en ambos miembros:
\[x_1 = x_2 \]Por lo tanto, \(h\) es inyectiva.
Ahora podemos buscar la inversa de \(h\):
\[y = \frac{3x - 4}{x + 1} \]Multiplicamos por \((x + 1)\) en ambos miembros:
\[y(x + 1) = 3x - 4 \]Distribuimos:
\[yx + y = 3x - 4 \]Restamos \(3x\) en ambos miembros:
\[yx - 3x + y = -4 \]Restamos \(y\) en ambos miembros:
\[yx - 3x = -y - 4 \]Aplicamos factor común de \(x\) en el primer miembro:
\[x(y - 3) = -y - 4 \]Dividimos por \((y - 3)\) en ambos miembros:
\[x = \frac{-y - 4}{y - 3} \]Intercambiamos el lugar de las variables:
\[y = \frac{-x - 4}{x - 3} \]La función inversa es \(h^{-1}(x) = \frac{-x - 4}{x - 3}\).
3.
Determinar si \(f : \mathbb{R} \rightarrow \mathbb{R}\), \(f(x) = x^3 + 2\) tiene inversa y encontrarla.
Para saber si \(f\) tiene inversa, debemos saber si es biyectiva.
\(f\) es inyectiva?
Evaluamos en \(x_1\) y \(x_2\), los igualamos:
\[f(x_1) = f(x_2) \]Luego, reemplazamos \(x\) por \(x_1\) y \(x_2\):
\[x_1^3 + 2 = x_2^3 + 2 \]Restamos 2 en ambos miembros:
\[x_1^3 = x_2^3 \]Tomamos la raíz cúbica de ambos miembros:
\[\sqrt[3]{x_1^3} = \sqrt[3]{x_2^3} \]Cancelamos las potencias:
\[x_1 = x_2 \]Por lo tanto, \(f\) es inyectiva.
\(f\) es sobreyectiva?
\(f(x)\) puede ser cualquier número real. Por lo tanto, \(Im\;f(x) = \mathbb{R}\).
Por lo tanto, \(f\) es sobreyectiva y biyectiva.
Ahora podemos buscar la inversa de \(f\):
\[y = x^3 + 2 \]Restamos 2 en ambos miembros:
\[y - 2 = x^3 \]Tomamos la raíz cúbica de ambos miembros:
\[\sqrt[3]{y - 2} = \sqrt[3]{x^3} \]Cancelamos la potencia:
\[\sqrt[3]{y - 2} = x \]Intercambiamos el lugar de las variables:
\[y = \sqrt[3]{x - 2} \]La función inversa es \(f^{-1}(x) = \sqrt[3]{x - 2}\).
Funciones Trigonométricas Inversas
Las funciones trigonométricas tienen inversa acorde al dominio y conjunto de salida.
Ejemplo: \(f : [0, \pi] \rightarrow [-1, 1]\), \(f(x) = \cos(x)\).
Los nombres de las funciones inversas son arc[nombre], como: \(\arccos(x)\) (arcocoseno)
Parábola
Las parábolas tienen tres formas distintas de escribirse:
- Polinómica: \(\;\;y = ax^2 + bx + c\)
- Factorizada: \(\;\;y = a(x - x_1)(x - x_2)\)
- Canónica: \(\;\;y = a(x - x_v)^2 + y_v\)
Circunferencia
Fórmula de la Circunferencia
La fórmula de la circunferencia es: \((x - x_0)^2 + (y - y_0)^2 = r^2\)
Donde \((x_0, y_0)\) es el centro de la circunferencia y \(r\) es el radio.
Ejercicios resueltos - Circunferencia
1.
Hallar la ecuación de la circunferencia con centro en \((2, -1)\) y radio \(r = 3\).
Sabiendo la anterior fórmula, reemplazamos los valores:
\[(x - 2)^2 + (y - (-1))^2 = 3^2 \]Resolvemos las partes necesarias:
\[(x - 2)^2 + (y + 1)^2 = 9 \]2.
Encontrar el centro y radio de la siguiente circunferencia: \(x^2 + y^2 - 4x + 6y + 4 = 0\).
El primer paso es agrupar los términos:
\[(x^2 - 4x) + (y^2 + 6y) + 4 = 0 \]Luego, completamos cuadrados (aplicando también la propiedad uniforme):
\[(x^2 - 4x + 2^2) + (y^2 + 6y + 3^2) + 4 = 0 + 2^2 + 3^2 \]Aplicamos cuadrado de un binomio (seguimos la fórmula original):
\[(x - 2)^2 + (y - (-3))^2 + 4 = 13 \]Restamos 4 en ambos miembros:
\[(x - 2)^2 + (y + 3)^2 = 9 \]Por lo tanto, el centro es \((2, -3)\), para calcular el radio sería: \(\sqrt{r^2} = \sqrt{9} \Rightarrow r = 3\)
3.
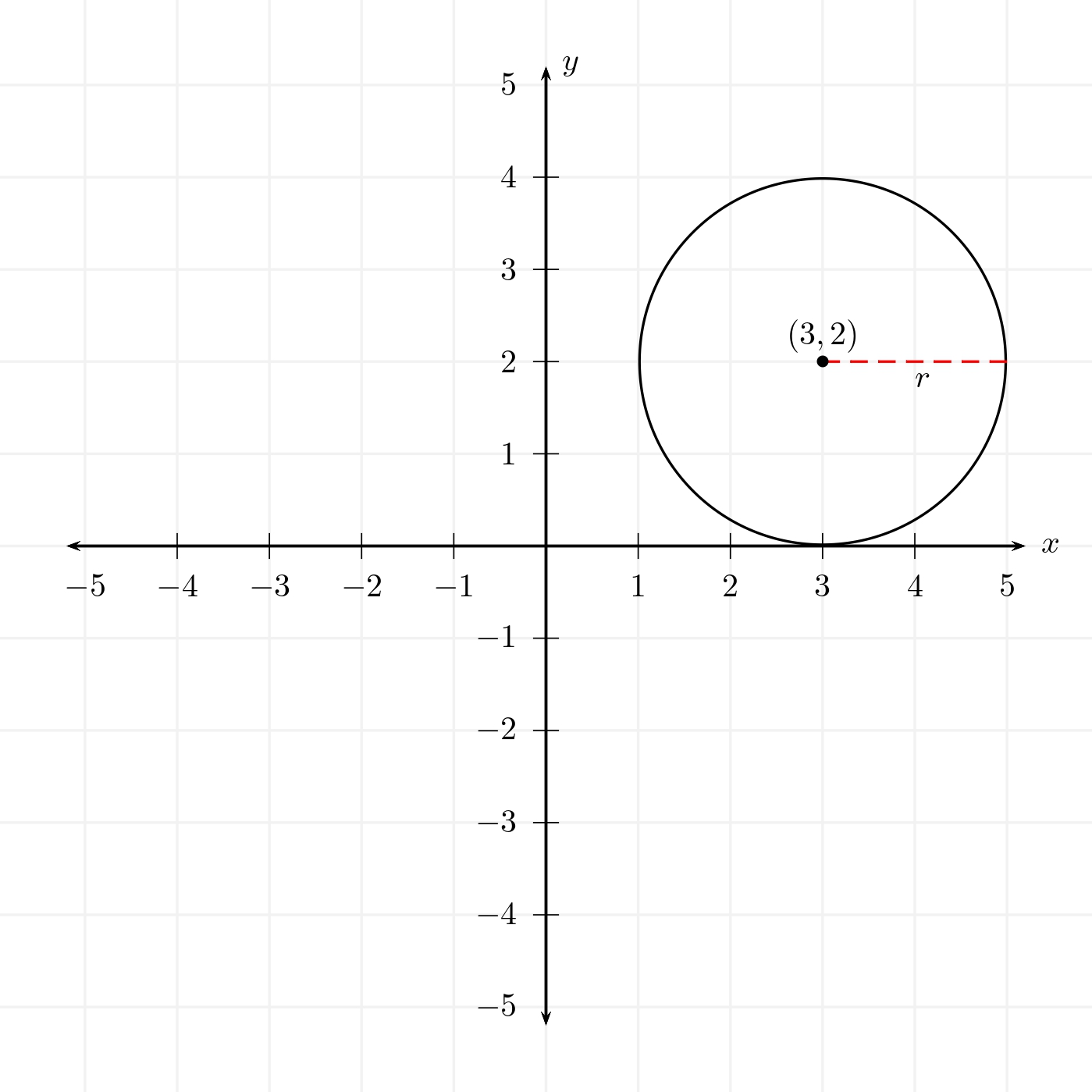
Graficar la circunferencia con centro en \((1, 2)\) y radio \(r = 2\).
El gráfico se vería de la siguiente manera:
Elipse
Fórmula de la Elipse
La fórmula de la elipse es: \(\frac{(x - x_0)^2}{a^2} + \frac{(y - y_0)^2}{b^2} = 1\)
Donde \((x_0, y_0)\) es el centro de la elipse, \(a\) y \(b\) son los semiejes.
Ejercicios resueltos - Elipse
1.
Hallar la ecuación de la elipse con centro en \((2, -1)\), semieje horizontal \(a = 3\) y semieje vertical \(b = 2\).
Sabiendo la anterior fórmula, reemplazamos los valores:
\[\frac{(x - 2)^2}{3^2} + \frac{(y - (-1))^2}{2^2} = 1 \]Resolvemos las partes necesarias:
\[\frac{(x - 2)^2}{9} + \frac{(y + 1)^2}{4} = 1 \]2.
Encontrar el centro y semiejes de la siguiente elipse: \(9x^2 + 5y^2 - 18x - 40y + 44 = 0\).
El primer paso es agrupar los términos:
\[(9x^2 - 18x) + (5y^2 - 40y) + 44 = 0 \]Ahora tenemos que deshacernos del coeficiente de \(x^2\) y \(y^2\), para eso factorizamos:
\[9(x^2 - 2x) + 5(y^2 - 8y) + 44 = 0 \]Luego, completamos cuadrados (aplicando también la propiedad uniforme):
\[9(x^2 - 2x + 1^2) + 5(y^2 - 8y + 4^2) + 44 = 0 + 9(1^2) + 5(4^2) \]Aplicamos cuadrado de un binomio:
\[9(x - 1)^2 + 5(y - 4)^2 + 44 = 89 \]Restamos 44 en ambos miembros:
\[9(x - 1)^2 + 5(y - 4)^2 = 45 \]Siguiendo la fórmula original, tenemos que igualar a 1. Para eso, dividimos en ambos miembros por 45:
\[\frac{9(x - 1)^2}{45} + \frac{5(y - 4)^2}{45} = \frac{45}{45} \]Simplificamos:
\[\frac{(x - 1)^2}{5} + \frac{(y - 4)^2}{9} = 1 \]Por lo tanto, el centro es \((1, 4)\), para calcular los semiejes sería: \(\sqrt{a^2} = \sqrt{5} \Rightarrow a = \sqrt{5},\; \sqrt{b^2} = \sqrt{9} \Rightarrow b = 3\)
Siendo en este caso \(a\) el semieje menor y \(b\) el semieje mayor.
3.
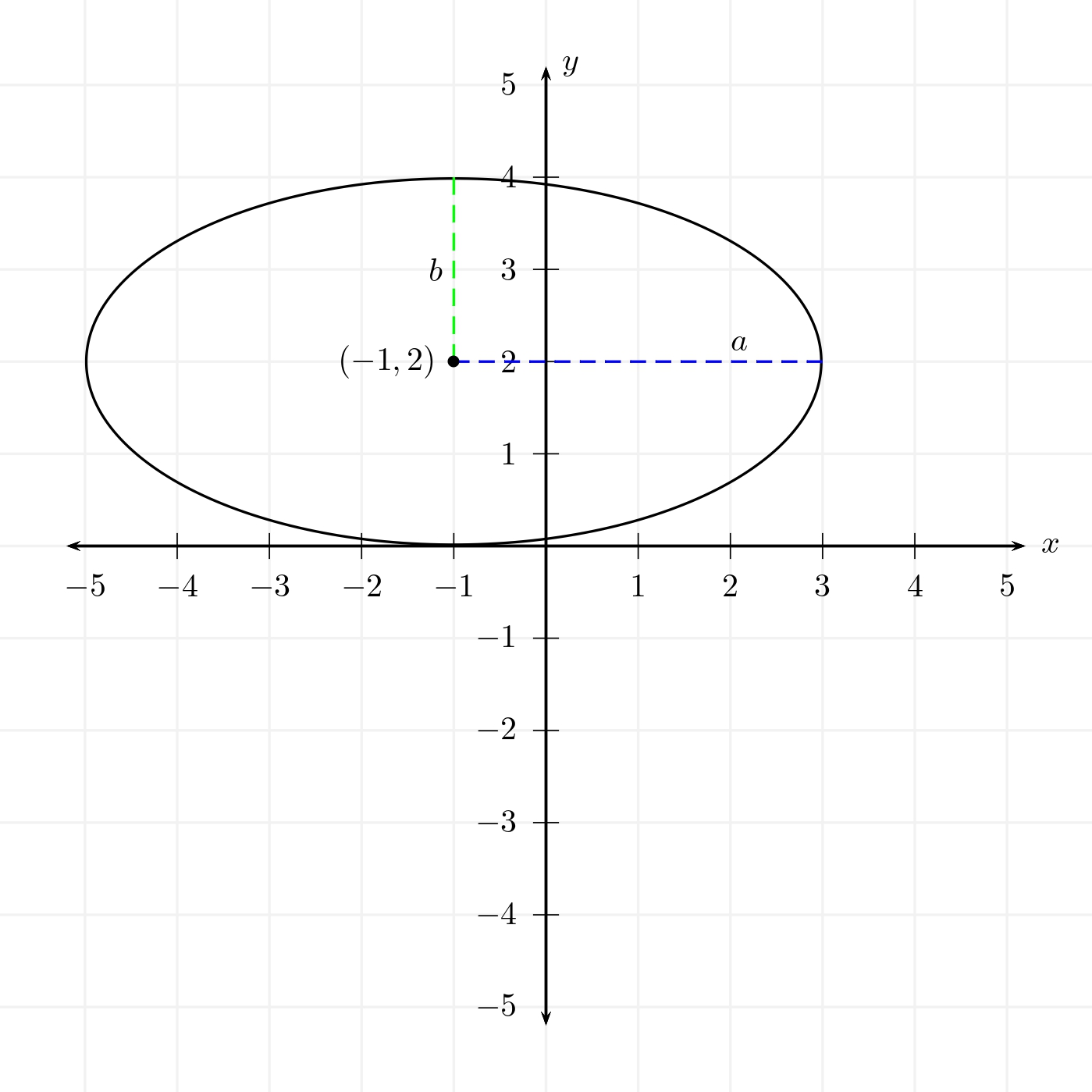
Graficar la elipse con centro en \((-1, 2)\), semieje horizontal \(a = 4\) y semieje vertical \(b = 2\).
El gráfico de la elipse es:
Función Exponencial y Logarítmica
La función exponencial de base \(a\) es \(f(x) = a^x\)
La función logarítmica de base \(a\) es \(f(x) = \log_a(x)\). Su dominio es \(\mathbb{R^+}\).
La función logarítmica es la inversa de la exponencial. Si tenemos \(f : \mathbb{R} \rightarrow \mathbb{R^+}\) y \(f(x) = a^x\), entonces \(f\) es biyectiva, por lo que \(f^{-1}(x) = \log_a(x)\).
El logaritmo natural es la función logarítmica de base \(e\). Suponiendo que \(f(x) = e^x\), entonces \(f^{-1}(x) = \\ln(x)\). El siguiente gráfico muestra la función exponencial y logarítmica:
Propiedades - Función exponencial
- \(a^{x + y} = a^x \cdot a^y\)
- \(a^{x - y} = \frac{a^x}{a^y}\)
- \(a^{xy} = (a^x)^y\)
- \(a^{-x} = (\frac{1}{a})^x\)
- \((ab)^x = a^x b^x\)
- \(a^{\frac{x}{y}} = \sqrt[y]{a^x}\)
Propiedades - Función logarítmica
Sea \(a > 1\):
- \(\log_a(xy) = \log_a(x) + \log_a(y)\)
- \(\log_a(\frac{x}{y}) = \log_a(x) - \log_a(y)\)
- \(\log_a(x^y) = y \cdot \log_a(x)\)
- \(\ln(x) = b \implies x = e^b\)
Ejercicios resueltos - Función exponencial y logarítmica
1.
Resolver la siguiente ecuación: \(2^{x + 1} = 8\)
Igualamos la base de la exponencial con la base del número:
\[2^{x + 1} = 2^3 \]Igualamos los exponentes (ya que las bases son iguales):
\[x + 1 = 3 \]Restamos 1 en ambos miembros:
\[x = 2 \]2.
Resolver la ecuación: \(\ln(x + 2) + \ln(x - 3) = \ln(2x - 1)\)
Para resolver esta ecuación, debemos pensar en los valores que \(x\) puede tomar (debe ser mayor a \(0\)):
\[(x + 2 > 0) \land (x - 3 > 0) \land (2x - 1 > 0) \] \[(x > -2) \land (x > 3) \land (x > \frac{1}{2}) \]Se cumplen todos los casos \(\iff x > -2\).
Ahora podemos resolver la ecuación:
\[\ln(x + 2) + \ln(x - 3) = \ln(2x - 1) \]Aplicamos la propiedad de la suma de logaritmos:
\[\ln((x + 2)(x - 3)) = \ln(2x - 1) \]Igualamos los argumentos de los logaritmos:
\[(x + 2)(x - 3) = 2x - 1 \]Multiplicamos:
\[x^2 - x - 6 = 2x - 1 \]Restamos \(2x\) y sumamos 1 en ambos miembros:
\[x^2 - 3x + 5 = 0 \]Resolvemos la ecuación cuadrática:
\[x = \frac{3 \pm \sqrt{(-3)^2 - 4(1)(5)}}{2(1)} \] \[x = \frac{3 \pm \sqrt{9 - 20}}{2} \] \[x = \frac{3 \pm \sqrt{-11}}{2} \] \[x = \frac{3 \pm 11i}{2} \]\(x\) no puede ser un número complejo, por lo que no hay solución.
3.
Resolver la ecuación: \(\sqrt[3]{\ln(x)} = \ln(\sqrt[3]{x})\)
Para resolver esta ecuación, debemos pensar en los valores que \(x\) puede tomar (debe ser mayor a \(0\)):
\[(\ln(x) > 0) \land (\sqrt[3]{x} > 0) \]Se cumplen los casos \(\iff x > 0\)
Podemos usar la propiedad de la potencia de un logaritmo:
\[\ln(\sqrt[3]{x}) = \ln(x^{\frac{1}{3}}) = \frac{1}{3} \cdot \ln(x) \]Reemplazamos en la ecuación:
\[\sqrt[3]{\ln(x)} = \frac{1}{3} \ln(x) \]Elevamos ambos miembros al cubo:
\[\ln(x) = \frac{1}{27} \ln(x)^3 \]Restamos \(\frac{1}{27} \ln(x)^3\) en ambos miembros:
\[\ln(x) - \frac{1}{27} \ln(x)^3 = 0 \]Factorizamos:
\[\ln(x)(1 - \frac{1}{27} \ln(x)^2) = 0 \]Si \(ab = 0 \Rightarrow a = 0\;\lor\;b = 0\):
\[\ln(x) = 0\;\lor\;1 - \frac{1}{27} \ln(x)^2 = 0 \]Resolvemos el primer caso:
\[\ln(x) = 0 \]Buscamos el valor de \(x\):
\[x = e^0 \] \[x = 1 \]Resolvemos el segundo caso:
\[1 - \frac{1}{27} \ln(x)^2 = 0 \] \[\frac{1}{27} \ln(x)^2 = 1 \] \[\ln(x)^2 = 27 \] \[\ln(x) = \pm \sqrt{27} \]Buscamos el valor de \(x\):
\[x = e^{\pm \sqrt{27}} \] \[x = e^{\sqrt{27}}\;\lor\;x = e^{-\sqrt{27}} \]Las soluciones posibles son: \(x = 1\;\lor\;x = e^{\sqrt{27}}\;\lor\;x = e^{-\sqrt{27}}\)