Test de Hipótesis

Una afirmación relacionada a una determinada población recibe el nombre de hipótesis estadística.
El procedimiento de toma de decisión sobre la hipótesis es el test de hipótesis, donde se juzga si una propiedad es compatible con lo observado en una $\mathbf{m.a.}$ de la población.

Pasos para realizar un test de hipótesis

Se formulan dos hipótesis estadísticas opuestas: hipótesis nula $H_0$ (o de no diferencia) e hipótesis alternativa $H_1$.

$H_0$ es la que se quiere contrastar y se opone a la investigación que se quiere realizar.
$H_1$ es la que se quiere demostrar, y está será cierta si los datos de la muestra rechazan a $H_0$.

A partir de la $\mathbf{m.a.}$ se elige un estadístico para rechazar (o no) $H_0$.

Aquellos valores del estadístico que forman parte de la región de rechazo de $H_0$ tienen poca probabilidad de ocurrir, los que estan en la región de no rechazo tienen una probabilidad alta de ocurrir.

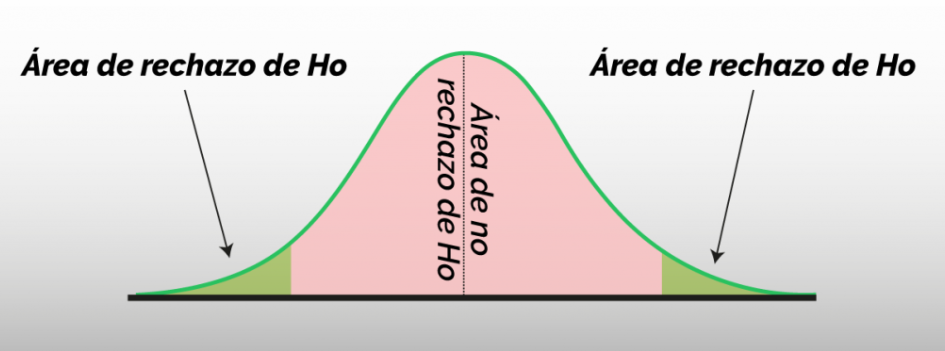
La suma de las áreas de rechazo es el error tipo I $\alpha$, es la probabilidad de rechazar $H_0$ cuando es cierta.

El error tipo II $\beta$ es la probabilidad aceptar $H_0$ cuando es falsa.

En base a toda esta información, los pasos a seguir son:

1. Definir $H_0, H_1$
2. Identificar prueba para validar $H_0$
3. Definir el nivel de significación $\alpha$
4. Calcular el valor $p$
5. Comparar el valor $p$ con $\alpha$ (si $p < \alpha$ se rechaza $H_0$ y se acepta $H_1$)

Dependiendo del planteo de $H_0$ y $H_1$ se pueden realizar diferentes tipos de pruebas (Chi-cuadrado, t-student, ANOVA, etc.)